k-nearest neighbors (knn)

2024-12-10

Motivation

Motivation

  • We are interested in estimating the conditional probability function:

\[ p(\mathbf{x}) = \mbox{Pr}(Y = 1 \mid X_1 = x_1, \dots, X_{784} = x_{784}). \]

Simpler example

Conditional Probability Function

Motivation

  • We are interested in estimating:

\[ p(\mathbf{x}) = \mbox{Pr}(Y = 1 \mid X_1 = x_1 , X_2 = x_2). \]

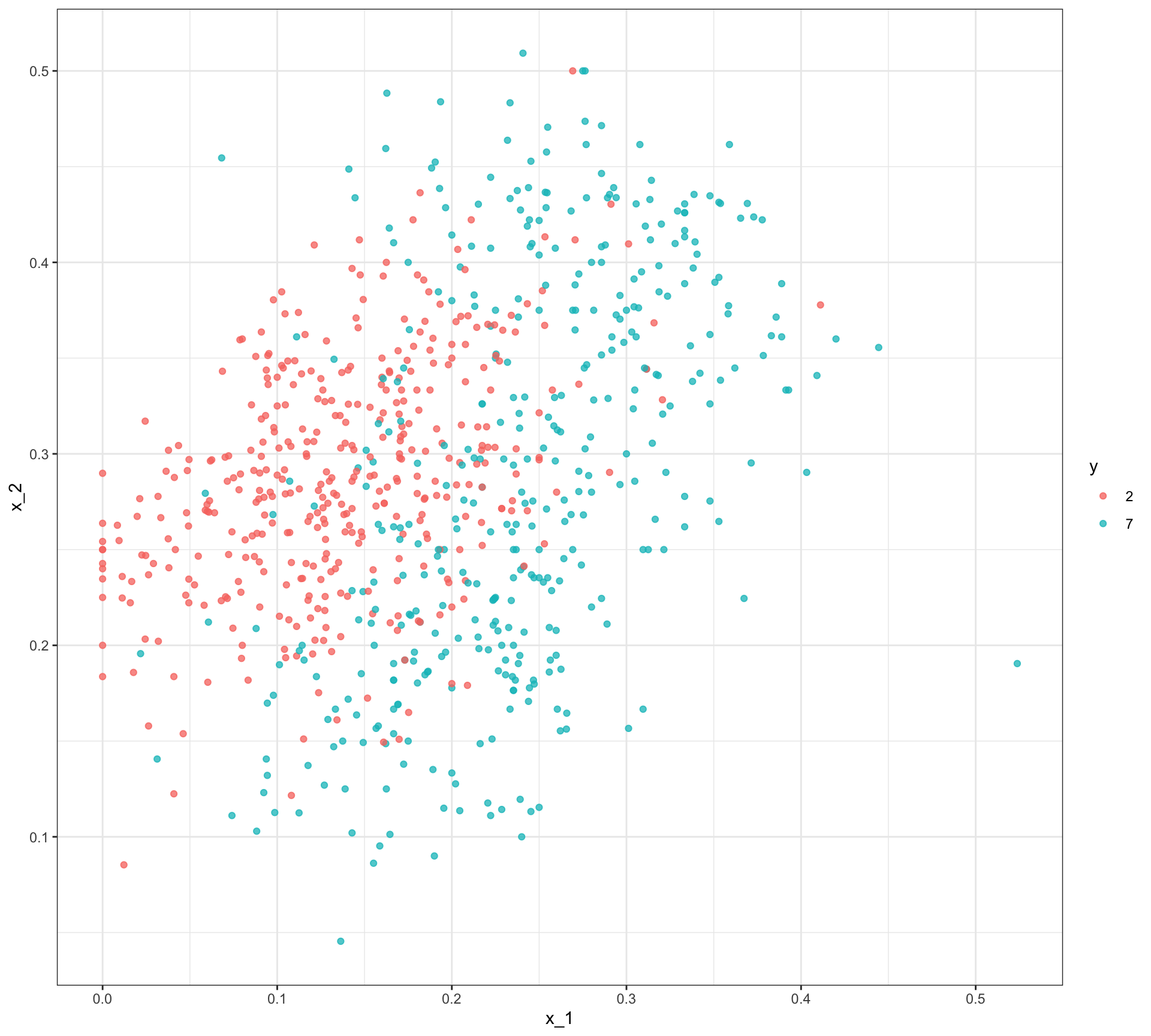
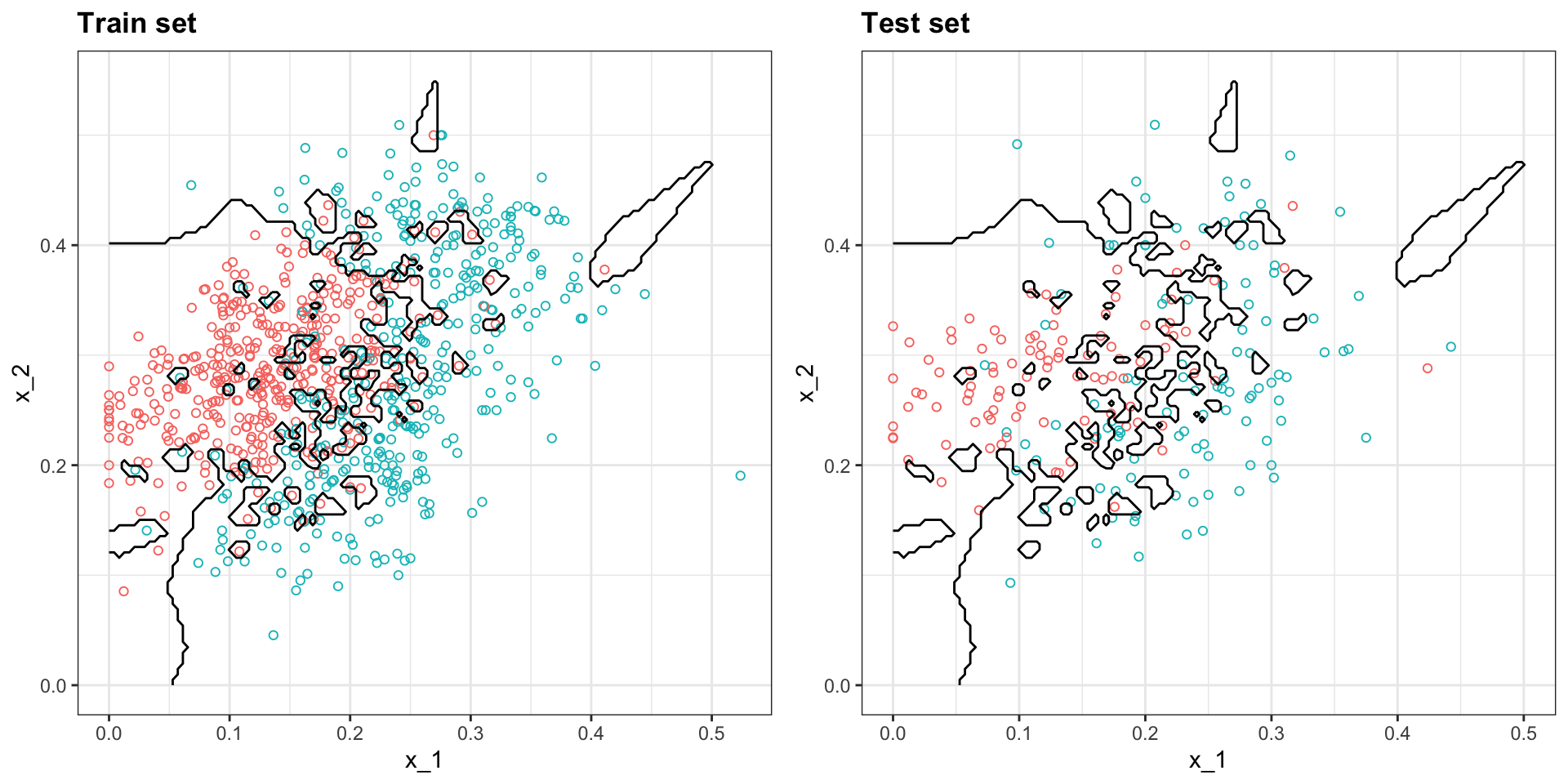
Training set

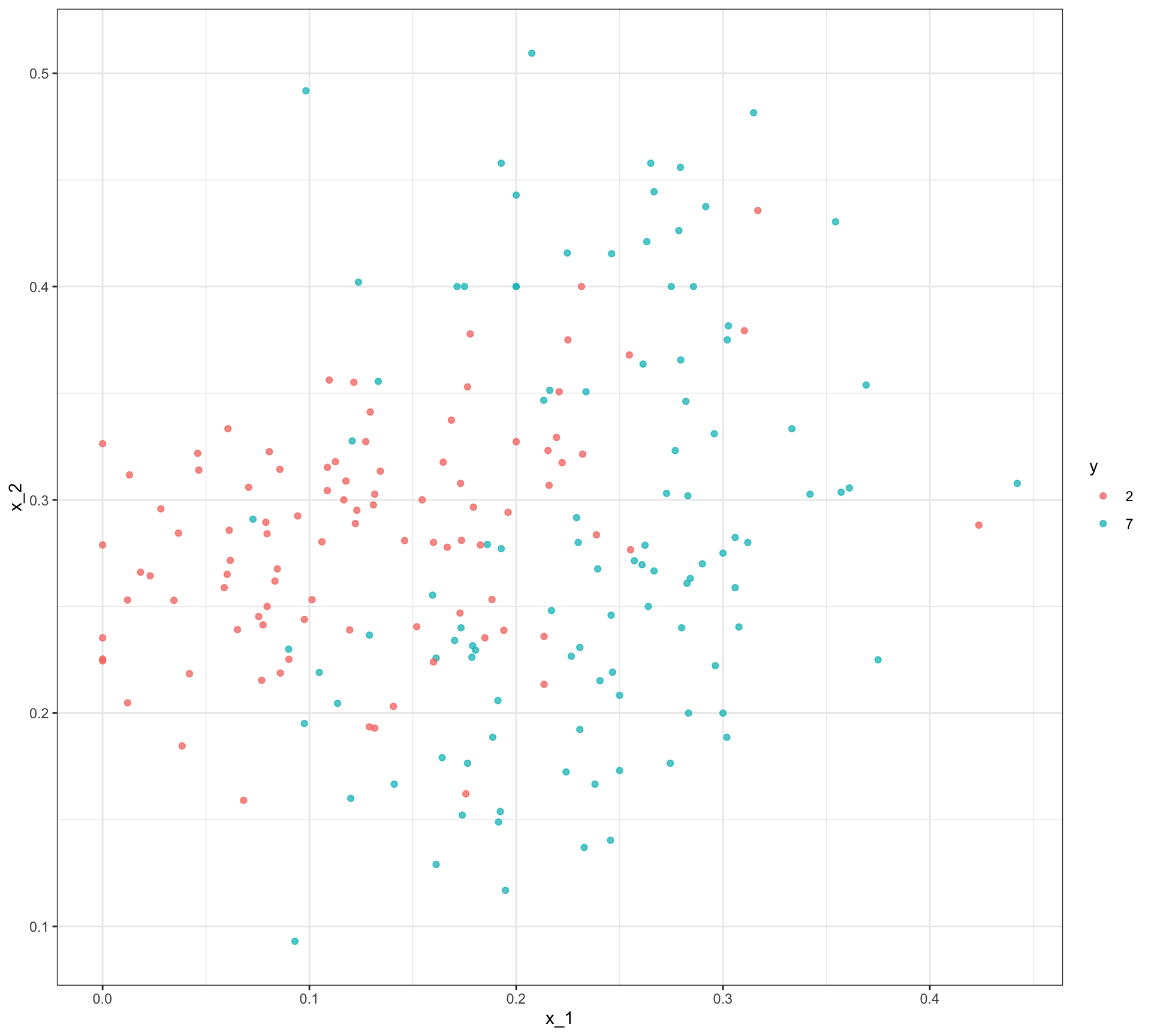
mnist_27$train |> ggplot(aes(x_1, x_2, color = y)) + geom_point(alpha=.75)

Test set

mnist_27$test |> ggplot(aes(x_1, x_2, color = y)) + geom_point(alpha = .75)

Motivation

  • With kNN we estimate \(p(\mathbf{x})\) using smoothing.

  • We define the distance between all observations based on the features.

  • For any \(\mathbf{x}_0\), we estimate \(p(\mathbf{x})\) by identifying the \(k\) nearest points to \(mathbf{x}_0\) and taking an average of the \(y\)s associated with these points.

  • We refer to the set of points used to compute the average as the neighborhood.

  • This gives us \(\widehat{p}(\mathbf{x}_0)\).

Motivation

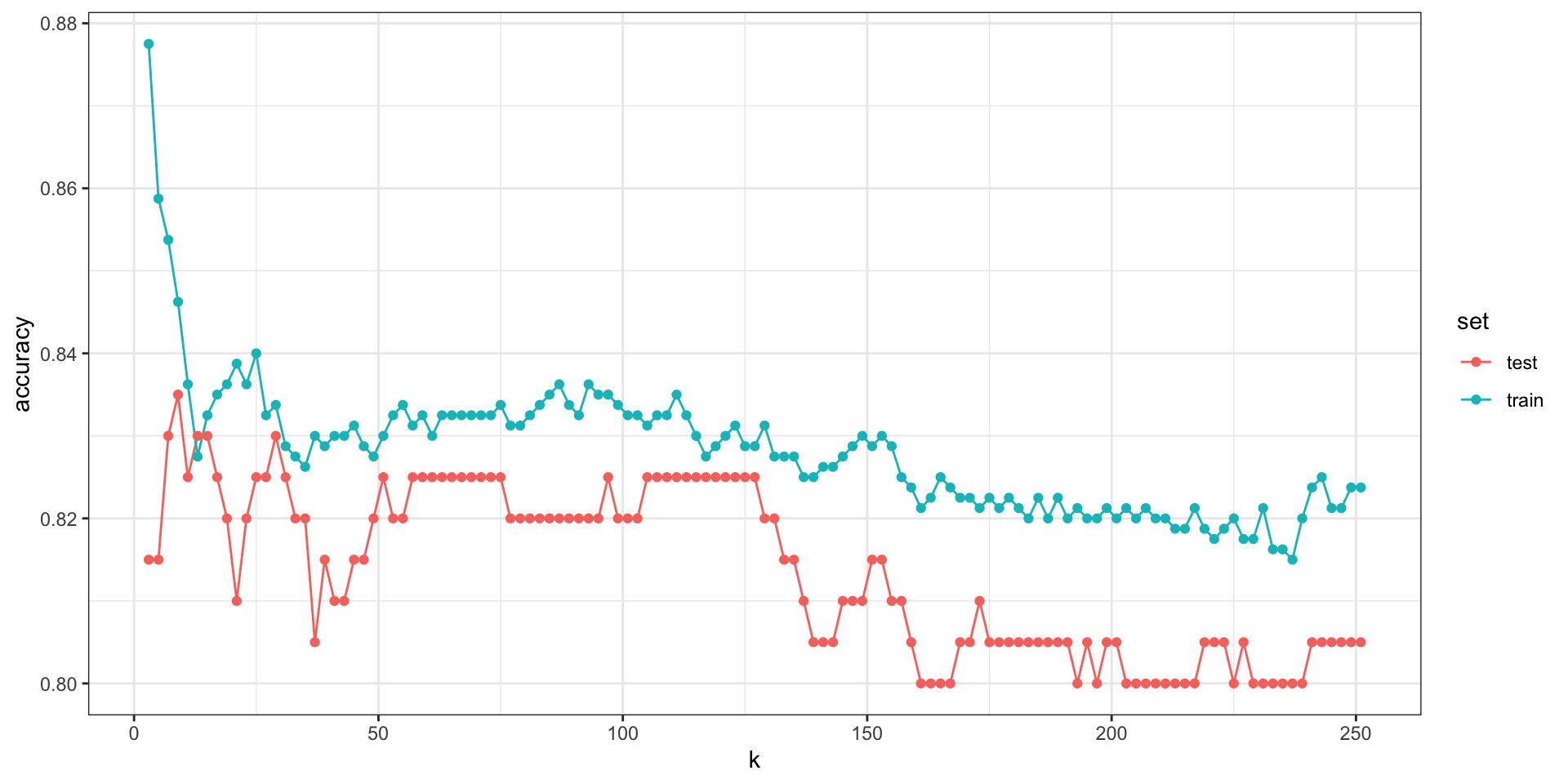
  • As with bin smoothers, we can control the flexibility of our estimate through the \(k\) parameter: larger \(k\)s result in smoother estimates, while smaller \(k\)s result in more flexible and wiggly estimates.

  • To implement the algorithm, we can use the knn3 function from the caret package.

  • Looking at the help file for this package, we see that we can call it in one of two ways.

  • We will use the first way in which we specify a formula and a data frame.

Let’s try it

library(dslabs) 
library(caret) 
knn_fit <- knn3(y ~ ., data = mnist_27$train, k = 5)

kNN

This gives us \(\widehat{p}(\mathbf{x})\):

p_hat_knn <- predict(knn_fit, mnist_27$test)[,2]
y_hat_knn <- predict(knn_fit, mnist_27$test, type = "class") 
confusionMatrix(y_hat_knn, mnist_27$test$y)$overall["Accuracy"] 
Accuracy 
   0.815
  • We see that kNN, with the default parameter, already beats regression.

kNN

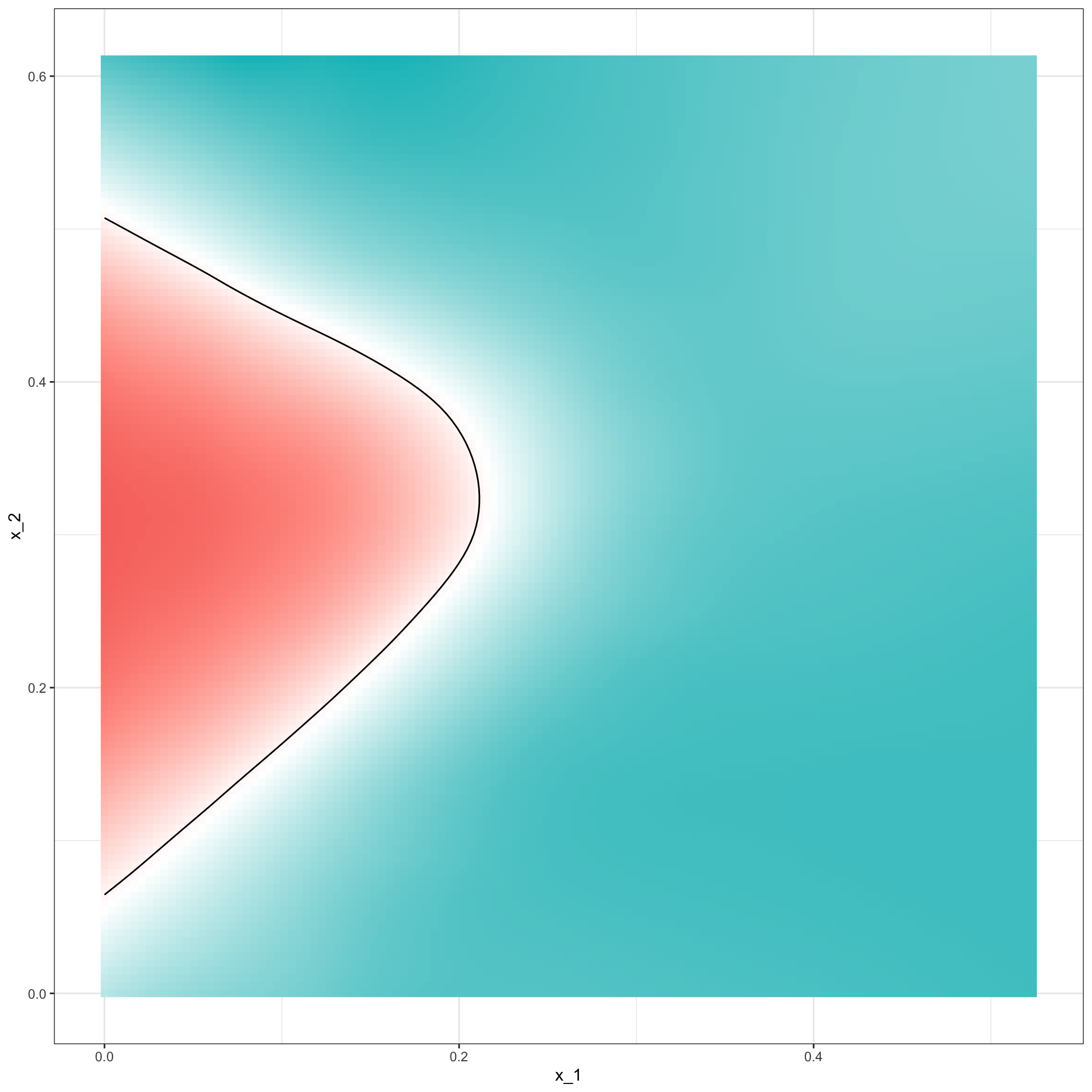
  • To see why this is the case, we plot \(\widehat{p}(\mathbf{x})\) and compare it to the true conditional probability \(p(\mathbf{x})\):

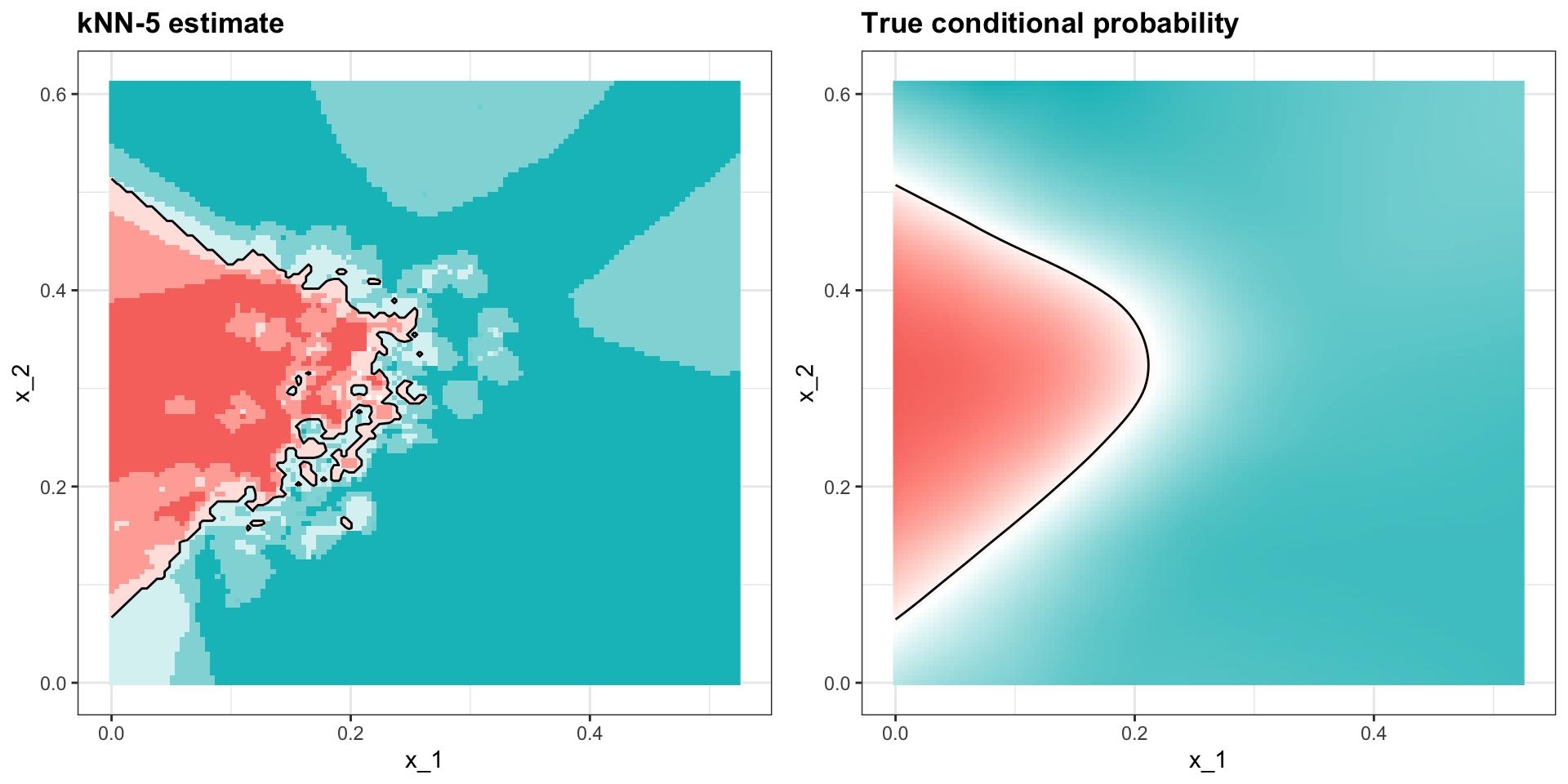
Over-training

Compare

y_hat_knn <- predict(knn_fit, mnist_27$train, type = "class") 
confusionMatrix(y_hat_knn, mnist_27$train$y)$overall["Accuracy"] 
Accuracy 
    0.86

to

y_hat_knn <- predict(knn_fit, mnist_27$test, type = "class") 
confusionMatrix(y_hat_knn, mnist_27$test$y)$overall["Accuracy"] 
Accuracy 
   0.815

Over-training

Compare this:

knn_fit_1 <- knn3(y ~ ., data = mnist_27$train, k = 1) 
y_hat_knn_1 <- predict(knn_fit_1, mnist_27$train, type = "class") 
confusionMatrix(y_hat_knn_1, mnist_27$train$y)$overall[["Accuracy"]] 
[1] 0.994

to this:

y_hat_knn_1 <- predict(knn_fit_1, mnist_27$test, type = "class") 
confusionMatrix(y_hat_knn_1, mnist_27$test$y)$overall["Accuracy"] 
Accuracy 
    0.81
  • We can see the over-fitting problem by plotting the decision rule boundaries produced by \(p(\mathbf{x})\):

Over-training

Over-smoothing

Let’s try a much bigger neighborhood:

knn_fit_401 <- knn3(y ~ ., data = mnist_27$train, k = 401) 
y_hat_knn_401 <- predict(knn_fit_401, mnist_27$test, type = "class") 
confusionMatrix(y_hat_knn_401, mnist_27$test$y)$overall["Accuracy"] 
Accuracy 
    0.76

Over-smoothing

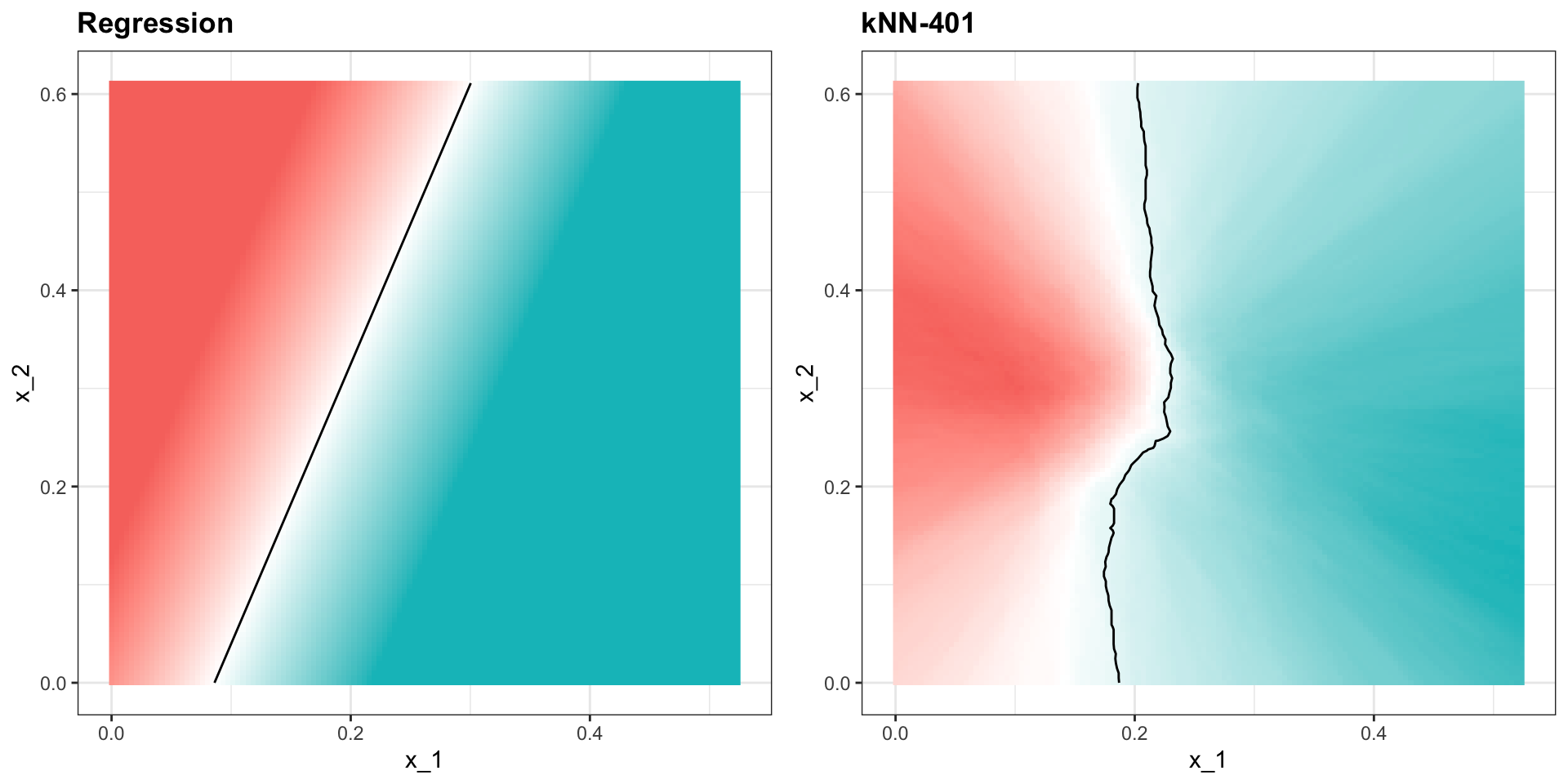
Parameter tuning