Confidence Intervals

2024-10-23

Confidence intervals

  • Confidence intervals are a very useful concept widely employed by data analysts.

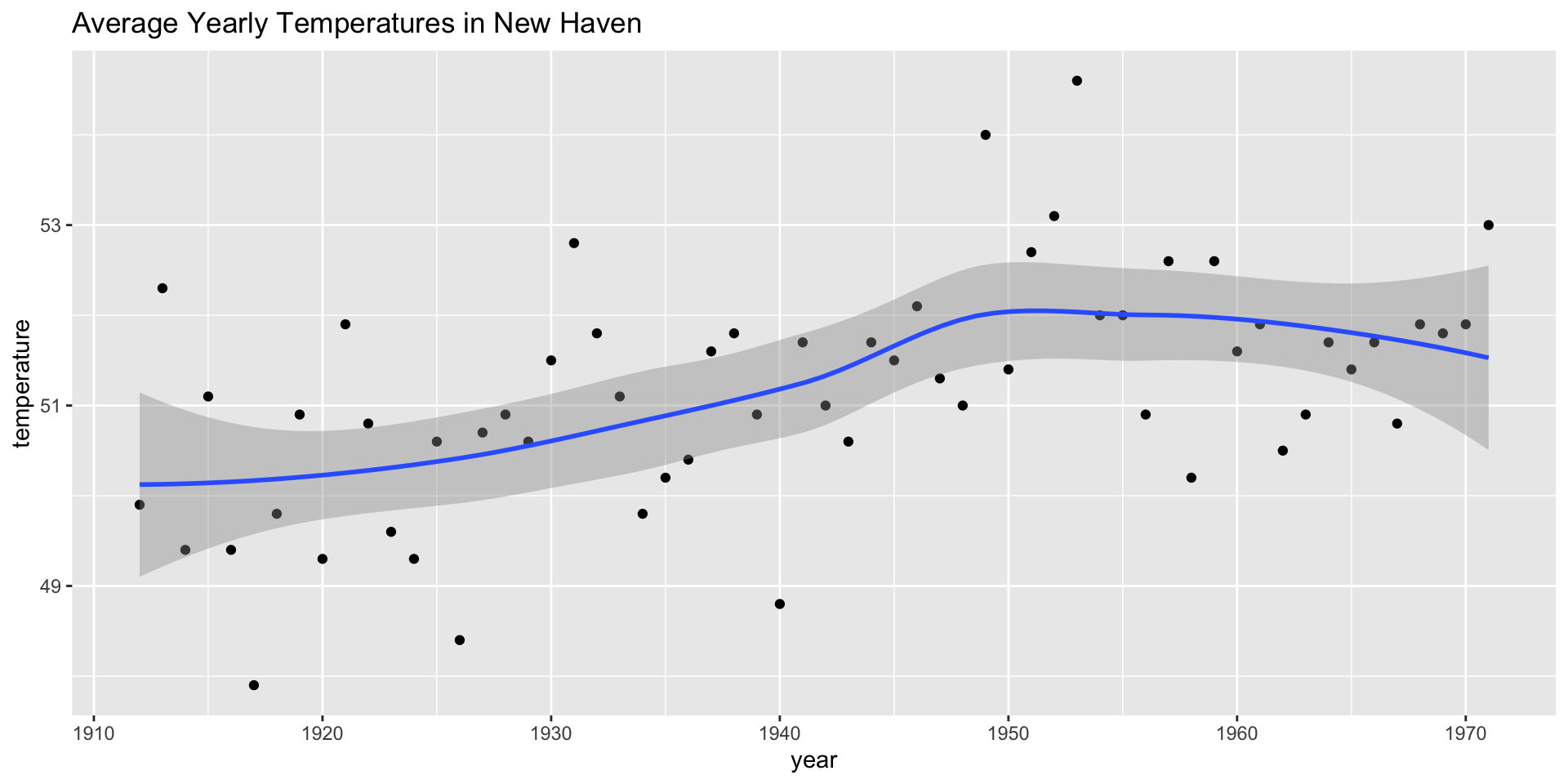
  • A version of these that are commonly seen come from the ggplot geometry geom_smooth.

  • Below is an example using a temperature dataset available in R:

Confidence intervals

Confidence intervals

  • In our competition, you were asked to give an interval.

  • If the interval you submitted includes the \(p\), you receive half the money you spent on your “poll” back and proceed to the next stage of the competition.

Confidence intervals

  • One way to pass to the second round is to report a very large interval.

  • For example, the interval \([0,1]\) is guaranteed to include \(p\).

  • However, with an interval this big, we have no chance of winning the competition.

Confidence intervals

  • Similarly, if you are an election forecaster and predict the spread will be between -100% and 100%, you will be ridiculed for stating the obvious.

  • Even a smaller interval, such as saying the spread will be between -10 and 10%, will not be considered serious.

Confidence intervals

  • On the other hand, the smaller the interval we report, the smaller our chances are of winning the prize.

  • Likewise, a bold pollster that reports very small intervals and misses the mark most of the time will not be considered a good pollster.

  • We might want to be somewhere in between.

  • We can use the statistical theory we have learned to compute the probability of any given interval including \(p\).

Confidence intervals

  • To illustrate this we run the Monte Carlo simulation.

  • We use the same parameters as above:

p <- 0.45 
N <- 1000

Confidence intervals

  • And notice that the interval here:
x <- sample(c(0, 1), size = N, replace = TRUE, prob = c(1 - p, p)) 
x_hat <- mean(x) 
se_hat <- sqrt(x_hat*(1 - x_hat)/N) 
c(x_hat - 1.96*se_hat, x_hat + 1.96*se_hat) 
[1] 0.4032809 0.4647191
  • is different from this one:
x <- sample(c(0,1), size = N, replace = TRUE, prob = c(1 - p, p)) 
x_hat <- mean(x) 
se_hat <- sqrt(x_hat*(1 - x_hat)/N) 
c(x_hat - 1.96*se_hat, x_hat + 1.96*se_hat) 
[1] 0.4301041 0.4918959
  • Keep sampling and creating intervals, and you will see the random variation.

Confidence intervals

  • To determine the probability that the interval includes \(p\), we need to compute the following:

\[ \mbox{Pr}\left(\bar{X} - 1.96\hat{\mbox{SE}}(\bar{X}) \leq p \leq \bar{X} + 1.96\hat{\mbox{SE}}(\bar{X})\right) \]

Confidence intervals

  • By subtracting and dividing the same quantities in all parts of the equation, we find that the above is equivalent to:

\[ \mbox{Pr}\left(-1.96 \leq \frac{\bar{X}- p}{\hat{\mbox{SE}}(\bar{X})} \leq 1.96\right) \]

Confidence intervals

  • The term in the middle is an approximately normal random variable with expected value 0 and standard error 1, which we have been denoting with \(Z\), so we have:

\[ \mbox{Pr}\left(-1.96 \leq Z \leq 1.96\right) \]

  • which we can quickly compute using :
pnorm(1.96) - pnorm(-1.96) 
[1] 0.9500042
  • proving that we have a 95% probability.

Confidence intervals

  • If we want to have a larger probability, say 99%, we need to multiply by whatever z satisfies the following:

\[ \mbox{Pr}\left(-z \leq Z \leq z\right) = 0.99 \]

  • We use:
z <- qnorm(0.995) 
z 
[1] 2.575829
pnorm(z) - pnorm(-z) 
[1] 0.99

Confidence intervals

  • In statistics textbooks, confidence interval formulas are given for arbitraty probabilities written as \(1-\alpha\).

  • We can obtain the \(z\) for the equation above using z = qnorm(1 - alpha / 2) because \(1 - \alpha/2 - \alpha/2 = 1 - \alpha\).

  • So, for example, for \(\alpha=0.05\), \(1 - \alpha/2 = 0.975\) and we get the \(z=1.96\) we used above:

qnorm(0.975) 
[1] 1.959964

A Monte Carlo simulation

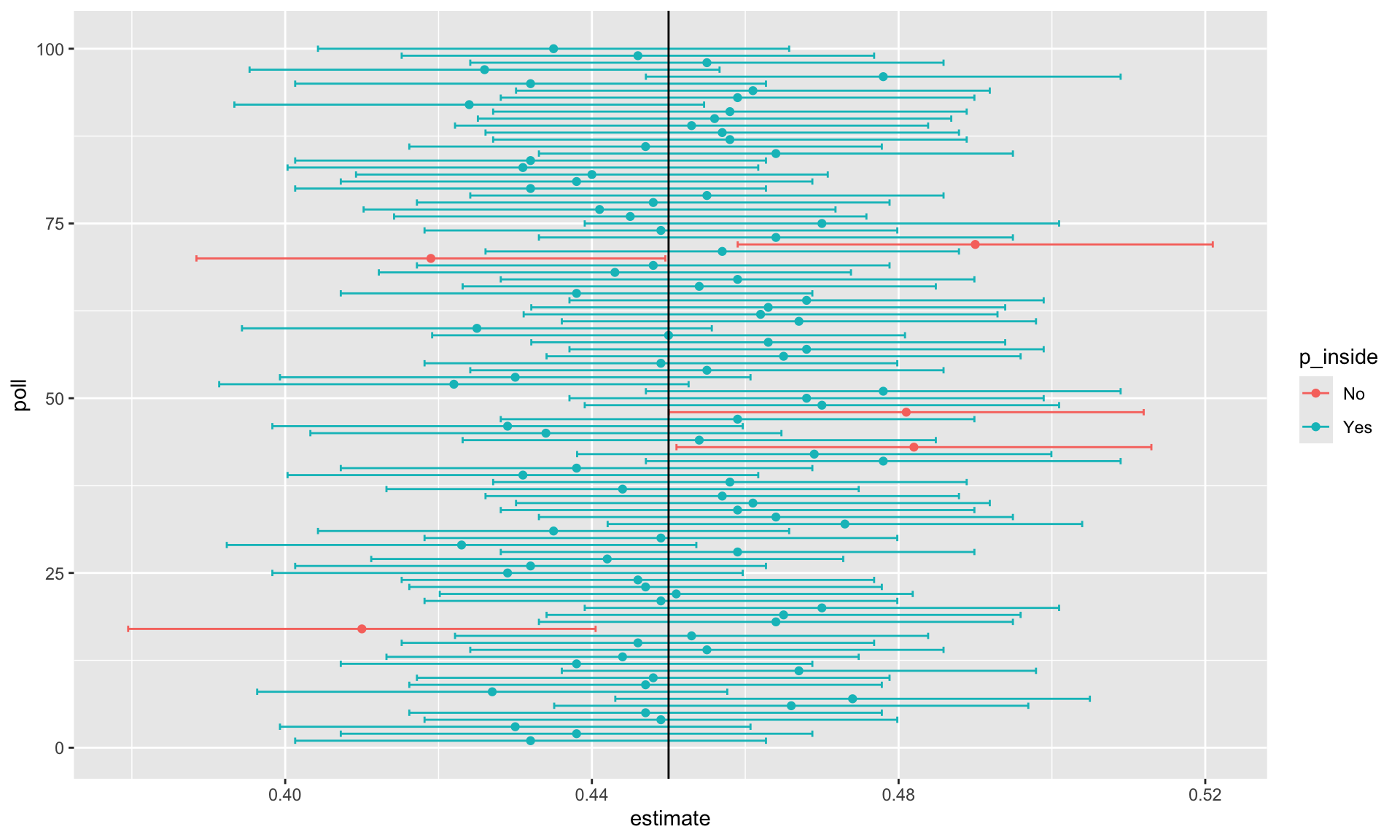
  • We can run a Monte Carlo simulation to confirm that, in fact, a 95% confidence interval includes \(p\) 95% of the time.
N <- 1000 
B <- 10000 
inside <- replicate(B, { 
  x <- sample(c(0,1), size = N, replace = TRUE, prob = c(1 - p, p)) 
  x_hat <- mean(x) 
  se_hat <- sqrt(x_hat*(1 - x_hat)/N) 
  between(p, x_hat - 1.96*se_hat, x_hat + 1.96*se_hat) 
}) 
mean(inside) 
[1] 0.9536

A Monte Carlo simulation

  • The following plot shows the first 100 confidence intervals.