Matrices In R

2024-11-12

Matrices in R

  • When the number of variables is large and they can all be represented as a number, it is convenient to store them in a matrix and perform the analysis with linear algebra operations, rather than using tidyverse with data frames.

  • Variables for each observation are stored in a row, resulting in a matrix with as many columns as variables.

  • We refer to values represented in the rows of the matrix as the covariates or predictors and, in machine learning, we refer to them as the features.

Matrices in R

  • In linear algebra, we have three types of objects: scalars, vectors, and matrices.

  • We have already learned about vectors in R, and, although there is no data type for scalars, we can represent them as vectors of length 1.

  • Today we learn how to work with matrices in R and relate them to linear algebra notation and concepts.

Case study: MNIST

  • The first step in handling mail received in the post office is to sort letters by zip code:

Case study: MNIST

  • Soon we will describe how we can build computer algorithms to read handwritten digits, which robots then use to sort the letters.

  • To do this, we first need to collect data, which in this case is a high-dimensional dataset and best stored in a matrix.

Case study: MNIST

Case study: MNIST

Examples:

Case study: MNIST

  • The images are converted into \(28 \times 28 = 784\) pixels:

Case study: MNIST

  • For each digitized image, indexed by \(i\), we are provided with 784 variables and a categorical outcome, or label, representing the digit among \(0, 1, 2, 3, 4, 5, 6, 7 , 8,\) and \(9\) that the image is representing.

  • Let’s load the data using the dslabs package:

library(tidyverse) 
library(dslabs) 
mnist <- read_mnist()

Case study: MNIST

  • In these cases, the pixel intensities are saved in a matrix:
class(mnist$train$images) 
[1] "matrix" "array"
  • The labels associated with each image are included in a vector:
table(mnist$train$labels) 

   0    1    2    3    4    5    6    7    8    9 
5923 6742 5958 6131 5842 5421 5918 6265 5851 5949

Motivating tasks

  1. Visualize the original image. The pixel intensities are provided as rows in a matrix.

  2. Do some digits require more ink to write than others?

  3. Are some pixels uninformative?

  4. Can we remove smudges?

  5. Binarize the data.

  6. Standardize the digits.

Motivating tasks

  • The tidyverse or data.table are not developed to perform these types of mathematical operations.

  • For this task, it is convenient to use matrices.

  • To simplify the code below, we will rename these x and y respectively:

x <- mnist$train$images 
y <- mnist$train$labels

Dimensions of a matrix

  • The nrow function tells us how many rows that matrix has:
nrow(x) 
[1] 60000

and ncol tells us how many columns:

ncol(x) 
[1] 784

Dimensions of a matrix

  • We learn that our dataset contains 60,000 observations (images) and 784 features (pixels).

  • The dim function returns the rows and columns:

dim(x) 
[1] 60000   784

Creating a matrix

  • We saw that we can create a matrix using the matrix function.
z <- matrix(rnorm(100*2), 100, 2)
  • Note that by default the matrix is filled in column by column:
matrix(1:15, 3, 5) 
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    7   10   13
[2,]    2    5    8   11   14
[3,]    3    6    9   12   15

Creating a matrix

  • To fill the matrix row by row, we can use the byrow argument:
matrix(1:15, 3, 5, byrow = TRUE) 
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    2    3    4    5
[2,]    6    7    8    9   10
[3,]   11   12   13   14   15

Creating a matrix

  • The function as.vector converts a matrix back into a vector:
as.vector(matrix(1:15, 3, 5)) 
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15

Warning

  • If the product of columns and rows does not match the length of the vector provided in the first argument, matrix recycles values.

  • If the length of the vector is a sub-multiple or multiple of the number of rows, this happens without warning:

matrix(1:3, 3, 5) 
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    1
[2,]    2    2    2    2    2
[3,]    3    3    3    3    3

Subsetting

  • To extract a specific entry from a matrix, for example the 300th row of the 100th column, we write:
x[300,100]

Subsetting

  • We can extract subsets of the matrices by using vectors of indexes.

  • For example, we can extract the first 100 pixels from the first 300 observations like this:

x[1:300,1:100]

Subsetting

  • To extract an entire row or subset of rows, we leave the column dimension blank.
x[1:300,]

Subsetting

  • Similarly, we can subset any number of columns by keeping the first dimension blank.

  • Here is the code to extract the first 100 pixels:

x[,1:100]

Warning

  • If we subset just one row or just one column, the resulting object is no longer a matrix.

  • For example:

dim(x[300,]) 
NULL
  • To avoid this, we can use the drop argument:
dim(x[100,,drop = FALSE]) 
[1]   1 784

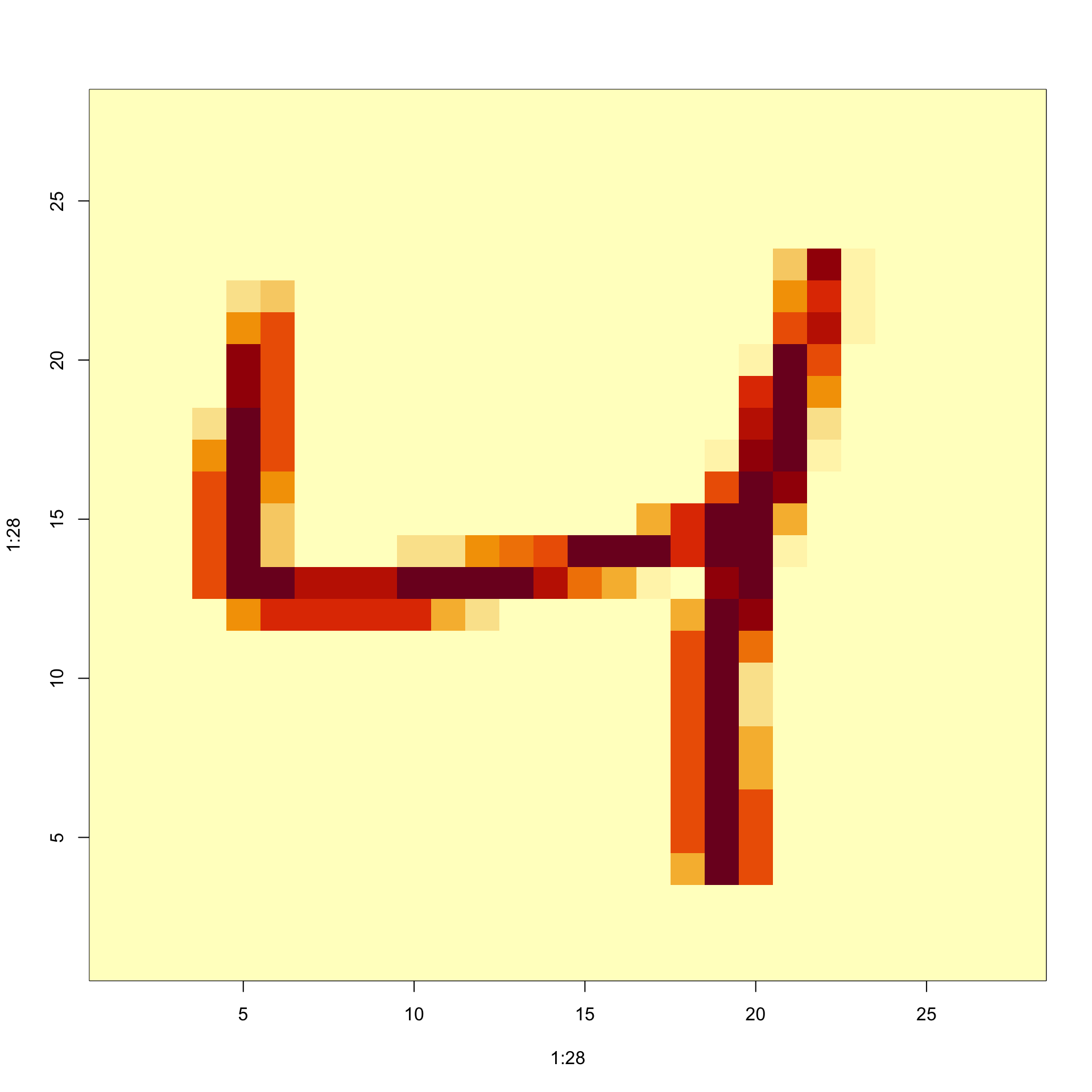
Visualize the original image

  • Let’s try to visualize the third observation.
mnist$train$label[3] 
[1] 4

Visualize the original image

  • The third row of the matrix x[3,] contains the 784 pixel intensities.

  • We can assume these were entered in order and convert them back to a \(28 \times 28\) matrix using:

grid <- matrix(x[3,], 28, 28)

Visualize the original image

  • To visualize the data, we can use image in the followin way:
image(1:28, 1:28, grid)

Visualize the original image

  • To flip it back we can use:
image(1:28, 1:28, grid[, 28:1])

Row and column summaries

  • A common operation with matrices is to apply the same function to each row or to each column.

  • For example, we may want to compute row averages and standard deviations.

  • The apply function lets you do this.

  • The first argument is the matrix, the second is the dimension, 1 for rows, 2 for columns, and the third is the function to be applied.

Row and column summaries

  • So, for example, to compute the averages and standard deviations of each row, we write:
avgs <- apply(x, 1, mean) 
sds <- apply(x, 1, sd)
  • To compute these for the columns, we simply change the 1 to a 2:
avgs <- apply(x, 2, mean) 
sds <- apply(x, 2, sd)

Row and column summaries

  • Because these operations are so common, special functions are available to perform them.

  • The functions rowMeans computes the average of each row:

avg <- rowMeans(x)
  • and the matrixStats function rowSds computes the standard deviations for each row:
library(matrixStats) 
sds <- rowSds(x)

Row and column summaries

  • The functions colMeans and colSds provide the version for columns.

  • For more fast implementations consider the functions available in matrixStats.

Do some digits require more ink to write than others?

  • For the second task, related to total pixel darkness, we want to see the average use of ink plotted against digit.

  • We have already computed this average and can generate a boxplot to answer the question:

avg <- rowMeans(x) 
boxplot(avg ~ y)

Do some digits require more ink to write than others?

Conditional filtering

  • One of the advantages of matrices operations over tidyverse operations is that we can easily select columns based on summaries of the columns.

  • Note that logical filters can be used to subset matrices in a similar way in which they can be used to subset vectors.

Conditional filtering

  • Here is a simple example subsetting columns with logicals:
matrix(1:15, 3, 5)[,c(FALSE, TRUE, TRUE, FALSE, TRUE)] 
     [,1] [,2] [,3]
[1,]    4    7   13
[2,]    5    8   14
[3,]    6    9   15
  • This implies that we can select rows with conditional expression.

Conditional filtering

  • In the following example we remove all observations containing at least one NA:
x[apply(!is.na(x), 1, all),]
  • This being a common operation, we have a matrixStats function to do it faster:
x[!rowAnyNAs(x),]

Are some pixels uninformative?

  • We can use these ideas to remove columns associated with pixels that don’t change much and thus do not inform digit classification.

  • We will quantify the variation of each pixel with its standard deviation across all entries.

Are some pixels uninformative?

  • Since each column represents a pixel, we use the colSds function from the matrixStats package:
sds <- colSds(x)

Are some pixels uninformative?

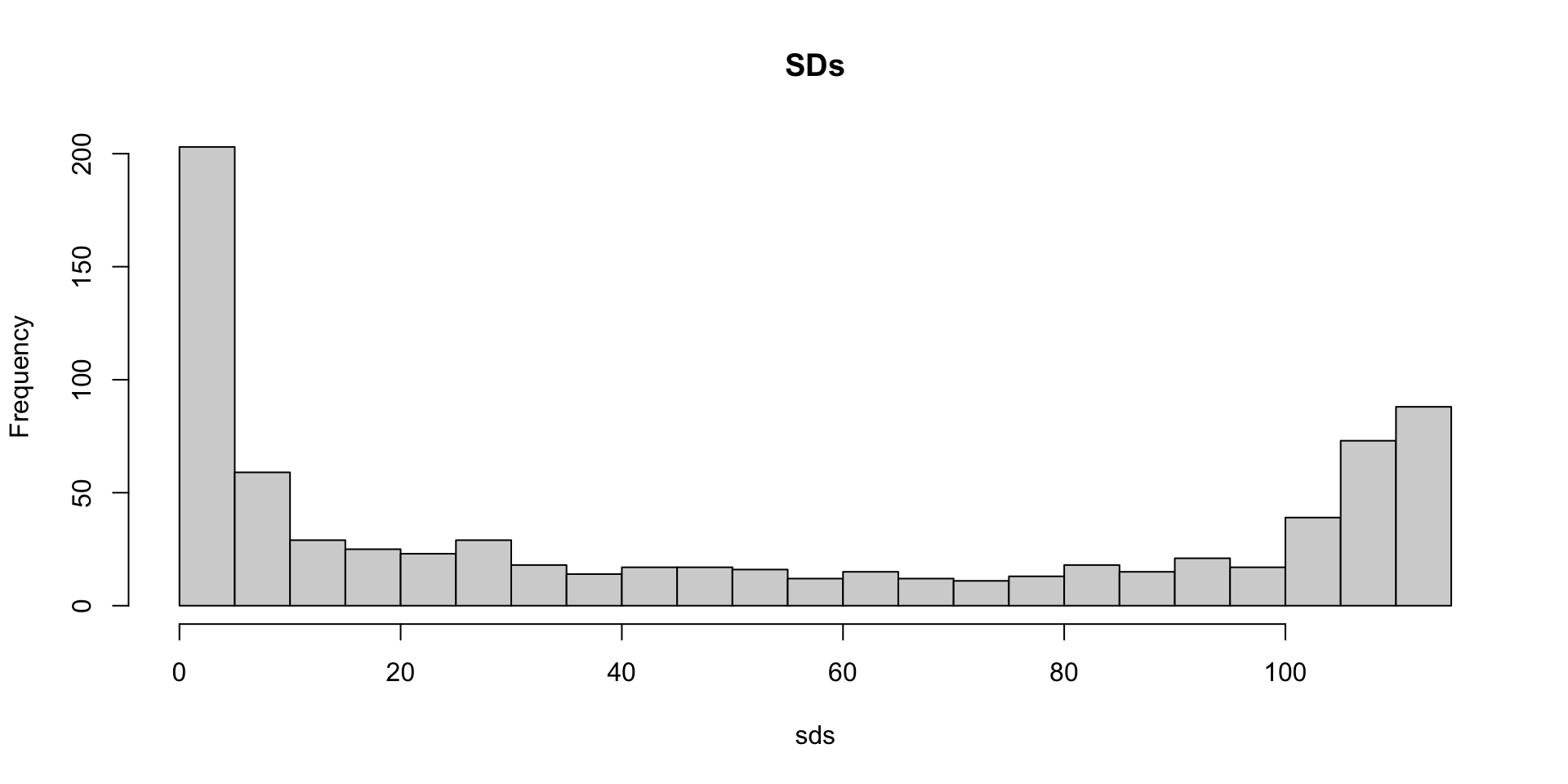
  • A quick look at the distribution of these values shows that some pixels have very low entry to entry variability:

Are some pixels uninformative?

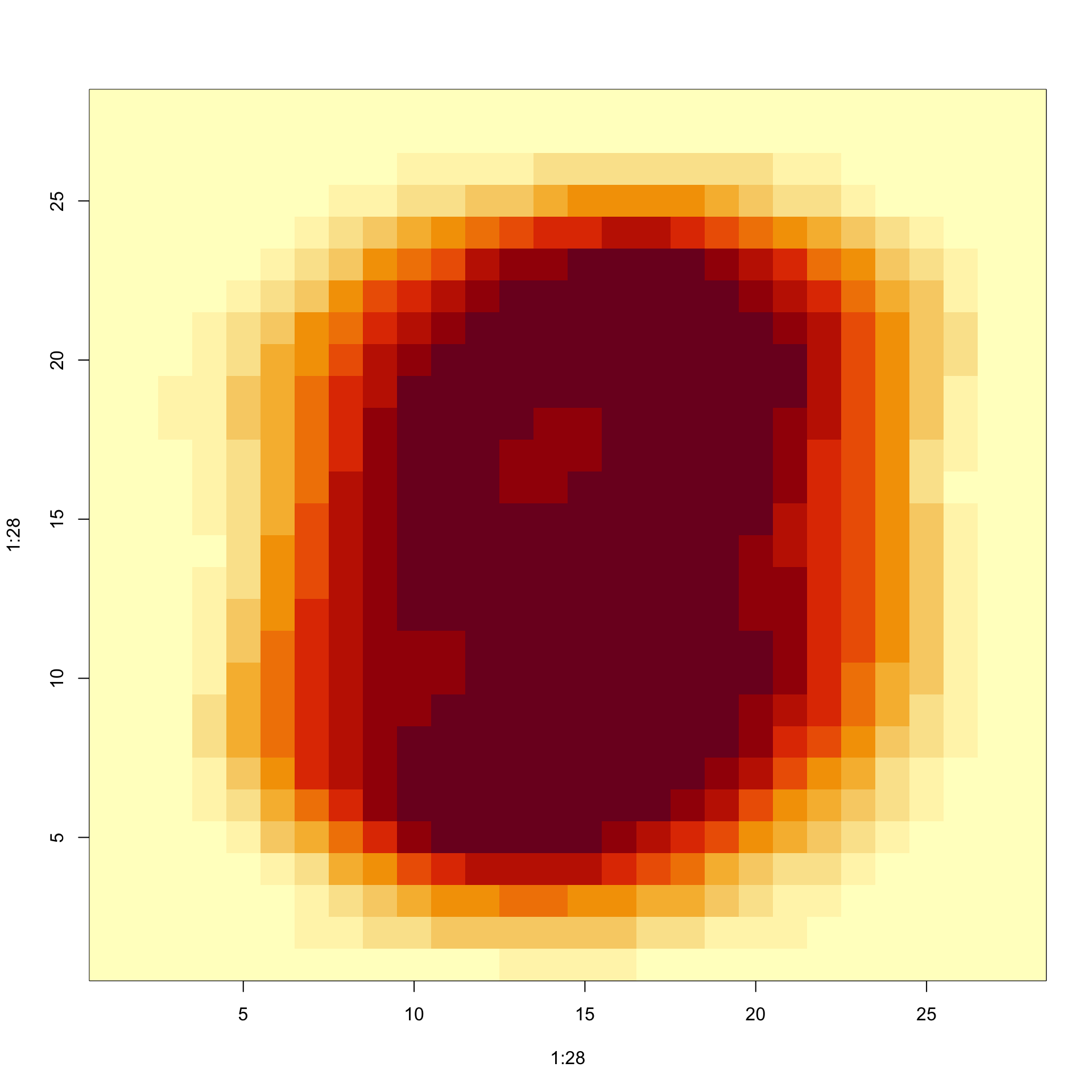
  • Here is the variance plotted by location:
image(1:28, 1:28, matrix(sds, 28, 28)[, 28:1])

Are some pixels uninformative?

  • We could remove features that have no variation since these can’t help us predict.

  • So if we wanted to remove uninformative predictors from our matrix, we could write this one line of code:

new_x <- x[,colSds(x) > 60] 
dim(new_x) 
[1] 60000   322
  • Only the columns for which the standard deviation is above 60 are kept, which removes over half the predictors.

Indexing with matrices

  • An operation that facilitates efficient coding is that we can change entries of a matrix based on conditionals applied to that same matrix.

  • Here is a simple example:

mat <- matrix(1:15, 3, 5) 
mat[mat > 6 & mat < 12] <- 0 
mat 
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    0    0   13
[2,]    2    5    0    0   14
[3,]    3    6    0   12   15

Indexing with matrices

  • A useful application is that we can change all the NA entries of a matrix to something else:
x[is.na(x)] <- 0

Can we remove smudges?

  • A histogram of all our predictor data:

Can we remove smudges?

  • The plot shows a clear dichotomy which is explained as parts of the image with ink and parts without.

  • If we think that values below, say, 50 are smudges, we can quickly make them zero using:

new_x <- x 
new_x[new_x < 50] <- 0

Binarizing the data

  • The previous histogram seems to suggest that this data is mostly binary.

  • A pixel either has ink or does not.

Binarizing the data

  • Applying what we have learned, we can binarize the data using just matrix operations:
bin_x <- x 
bin_x[bin_x < 255/2] <- 0  
bin_x[bin_x > 255/2] <- 1

Binarizing the data

  • We can also convert to a matrix of logicals and then coerce to numbers like this:
bin_X <- (x > 255/2)*1

Vectorization for matrices

  • In R, if we subtract a vector from a matrix, the first element of the vector is subtracted from the first row, the second element from the second row, and so on.

Vectorization for matrices

  • Using mathematical notation, we would write it as follows:

\[ \begin{bmatrix} X_{1,1}&\dots & X_{1,p} \\ X_{2,1}&\dots & X_{2,p} \\ & \vdots & \\ X_{n,1}&\dots & X_{n,p} \end{bmatrix} - \begin{bmatrix} a_1\\\ a_2\\\ \vdots\\\ a_n \end{bmatrix} = \begin{bmatrix} X_{1,1}-a_1&\dots & X_{1,p} -a_1\\ X_{2,1}-a_2&\dots & X_{2,p} -a_2\\ & \vdots & \\ X_{n,1}-a_n&\dots & X_{n,p} -a_n \end{bmatrix} \]

Vectorization for matrices

  • The same holds true for other arithmetic operations.

  • The function sweep facilitates this type of operation.

  • It works similarly to apply.

  • It takes each entry of a vector and applies an arithmetic operation to the corresponding row.

Vectorization for matrices

  • Subtraction is the default arithmetic operation.

  • So, for example, to center each row around the average, we can use:

sweep(x, 1, rowMeans(x))

Standardize the digits

  • The way R vectorizes arithmetic operations implies that we can scale each row of a matrix as follows:
(x - rowMeans(x))/rowSds(x)

Standardize the digits

  • Yet this approach does not work for columns.

  • For columns, we can sweep:

x_mean_0 <- sweep(x, 2, colMeans(x))

Standardize the digits

  • To divide by the standard deviation, we change the default arithmetic operation to division as follows:
x_standardized <- sweep(x_mean_0, 2, colSds(x), FUN = "/")

Componentwise multiplication

  • In R, if you add, subtract, multiple or divide two matrices, the operation is done elementwise.

  • For example, if two matrices are stored in x and y, then:

x*y

  • does not result in matrix multiplication.

  • Instead, the entry in row \(i\) and column \(j\) of this product is the product of the entry in row \(i\) and column \(j\) of x and y, respectively.