Distributions

2024-10-09

Visualizing data distributions

  • Summarizing complex datasets is crucial in data analysis, allowing us to share insights drawn from the data more effectively.

  • One common method is to use the average value to summarize a list of numbers.

  • For instance, a high school’s quality might be represented by the average score in a standardized test.

  • Sometimes, an additional value, the standard deviation, is added.

Visualizing data distributions

  • So, a report might say the scores were 680 \(\pm\) 50, boiling down a full set of scores to just two numbers.

  • But is this enough? Are we overlooking crucial information by relying solely on these summaries instead of the complete data?

  • Our first data visualization building block is learning to summarize lists of numbers or categories.

  • More often than not, the best way to share or explore these summaries is through data visualization.

Visualizing data distributions

  • The most basic statistical summary of a list of objects or numbers is its distribution.

  • Once a data has been summarized as a distribution, there are several data visualization techniques to effectively relay this information.

  • Understanding distributions is therefore essential for creating useful data visualizations.

  • Note: understanding distributions is also essential for understanding inference and statistical models

Case study: describing student heights

  • Pretend that we have to describe the heights of our classmates to someone that has never seen humans.

  • We ask students to report their height in inches.

  • We also ask them to report sex because there are two different height distributions.

     sex height
1   Male     75
2   Male     70
3   Male     68
4   Male     74
5   Male     61
6 Female     65

Case study

  • One way to convey the heights to ET is to simply send him this list of 1,050 heights.

  • But there are much more effective ways to convey this information, and understanding the concept of a distribution will be key.

  • To simplify the explanation, we first focus on male heights.

  • We examine the female height data later.

Distributions

  • The most basic statistical summary of a list of objects or numbers is its distribution.

  • For example, with categorical data, the distribution simply describes the proportion of each unique category:


Female   Male 
 0.227  0.773

Distributions

  • To visualize this we simply use a barplot.

  • Here is an example with US state regions:

Histograms

  • When the data is numerical, the task of displaying distributions is more challenging.

  • When data is not categorical, reporting the frequency of each entry, as we did for categorical data, is not an effective summary since most entries are unique.

  • For example, in our case study, while several students reported a height of 68 inches, only one student reported a height of 68.503937007874 inches and only one student reported a height 68.8976377952756 inches.

Histograms

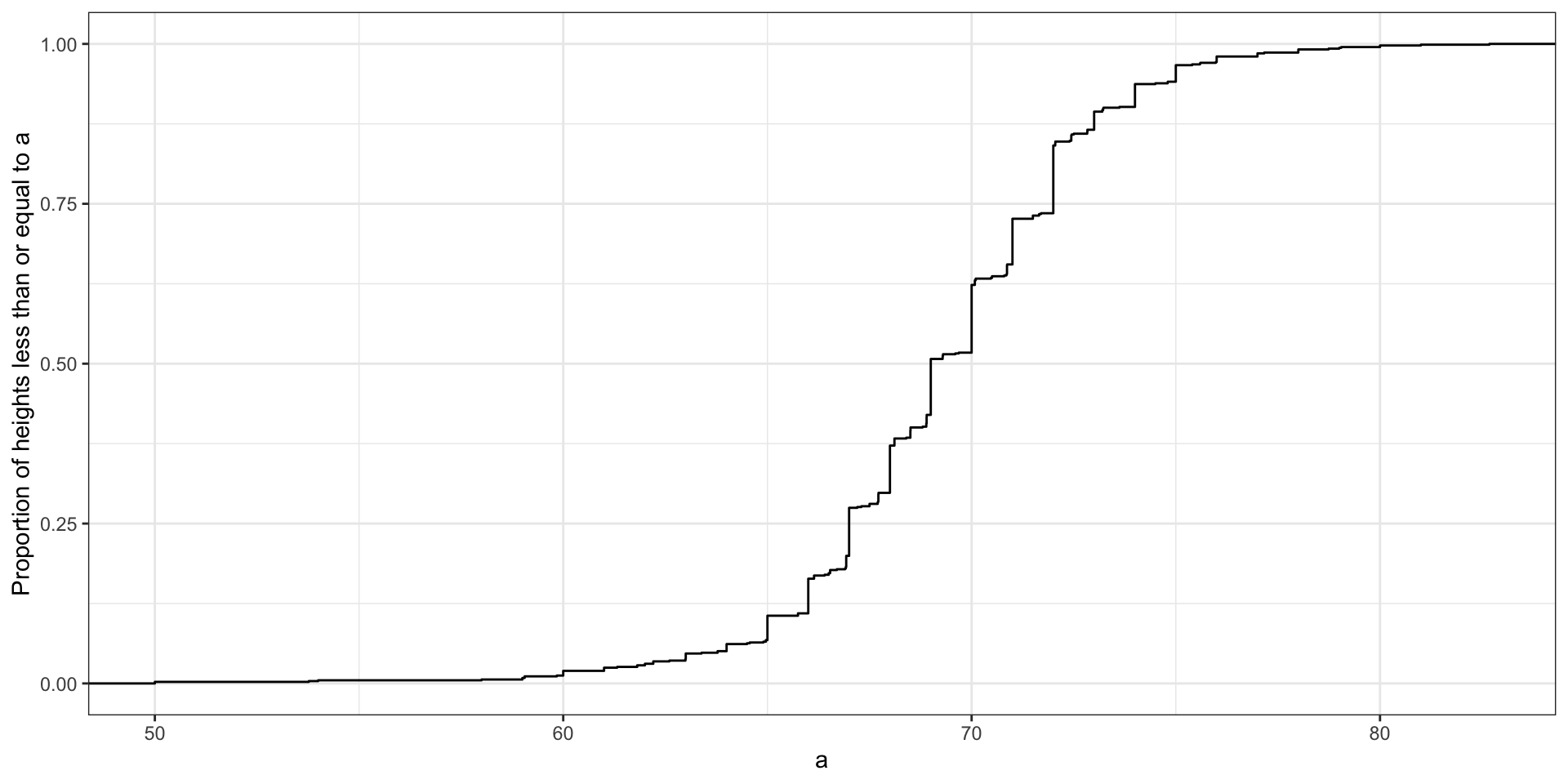
  • A more useful way to define a distribution for numeric data is to define a function that reports the proportion of the data below \(a\) for all possible values of \(a\).

  • This function is called the empirical cumulative distribution function (eCDF), it can be plotted, and it provides a full description of the distribution of our data.

Histograms

  • Here is the eCDF for male student heights:

Histograms

  • However, summarizing data by plotting the eCDF is actually not very popular in practice.

  • The main reason is that it does not easily convey characteristics of interest such as: at what value is the distribution centered? Is the distribution symmetric? What ranges contain 95% of the values?

  • Histograms sacrifice just a bit of information to produce plots that are much easier to interpret.

Histograms

Here is the histogram for the height data splitting the range of values into one inch intervals: \((49.5, 50.5]\), \((50.5, 51.5]\), \((51.5,52.5]\), \((52.5,53.5]\), \(...\), \((82.5,83.5]\).

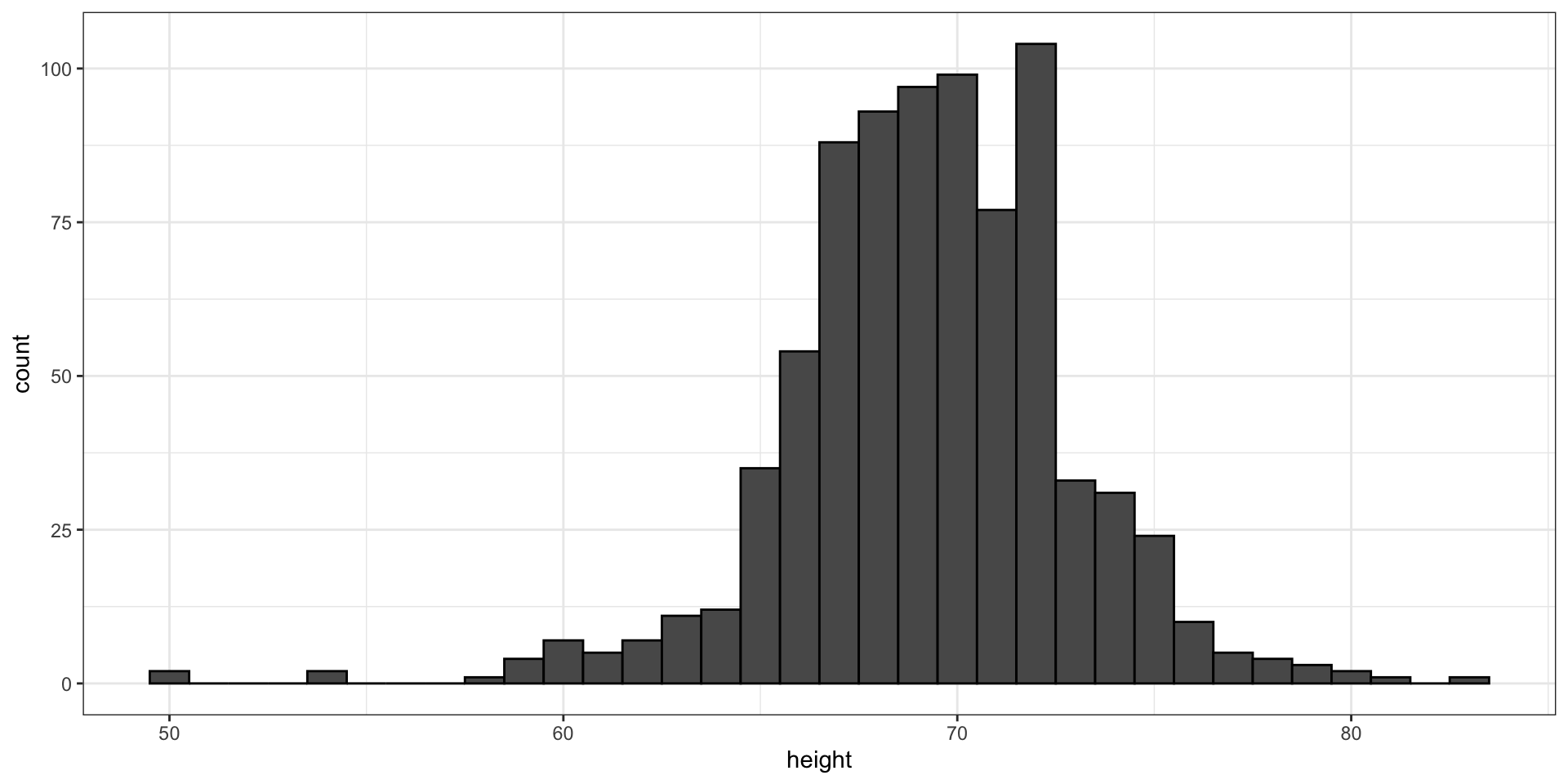
  • From this plot one immediately learn some important properties about our data.

Smoothed density

  • Smooth density plots relay the same information as a histogram but are aesthetically more appealing:

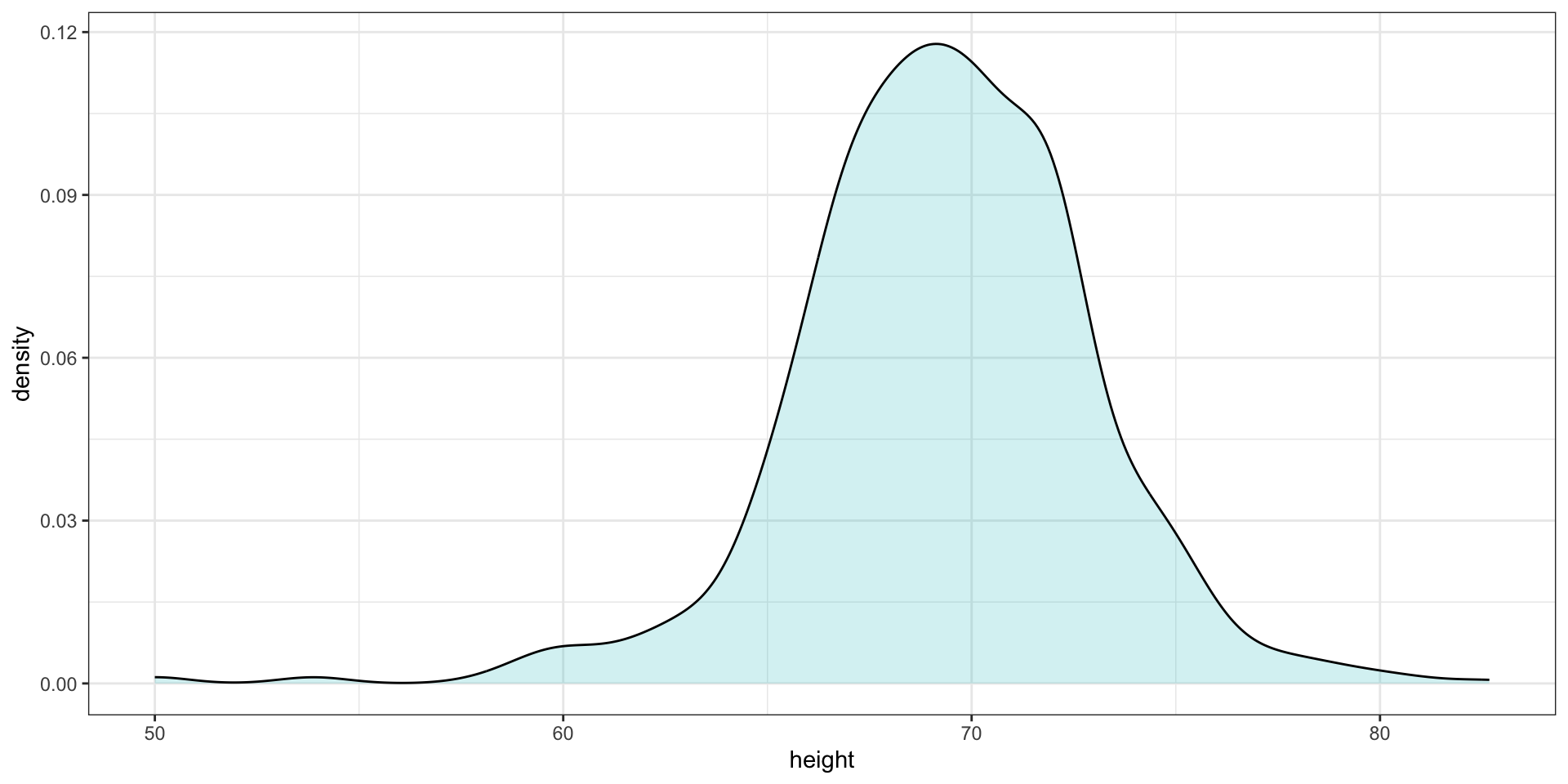
Smoothed density

  • In this plot, we no longer have sharp edges at the interval boundaries and many of the local peaks have been removed.

  • The scale of the y-axis changed from counts to density. Values shown y-axis are chosen so that the area under the curve adds up to 1.

  • To fully understand smooth densities, we have to understand estimates, a concept we cover later in the course.

Smoothed density

  • Here is an example comparing male and female heights:

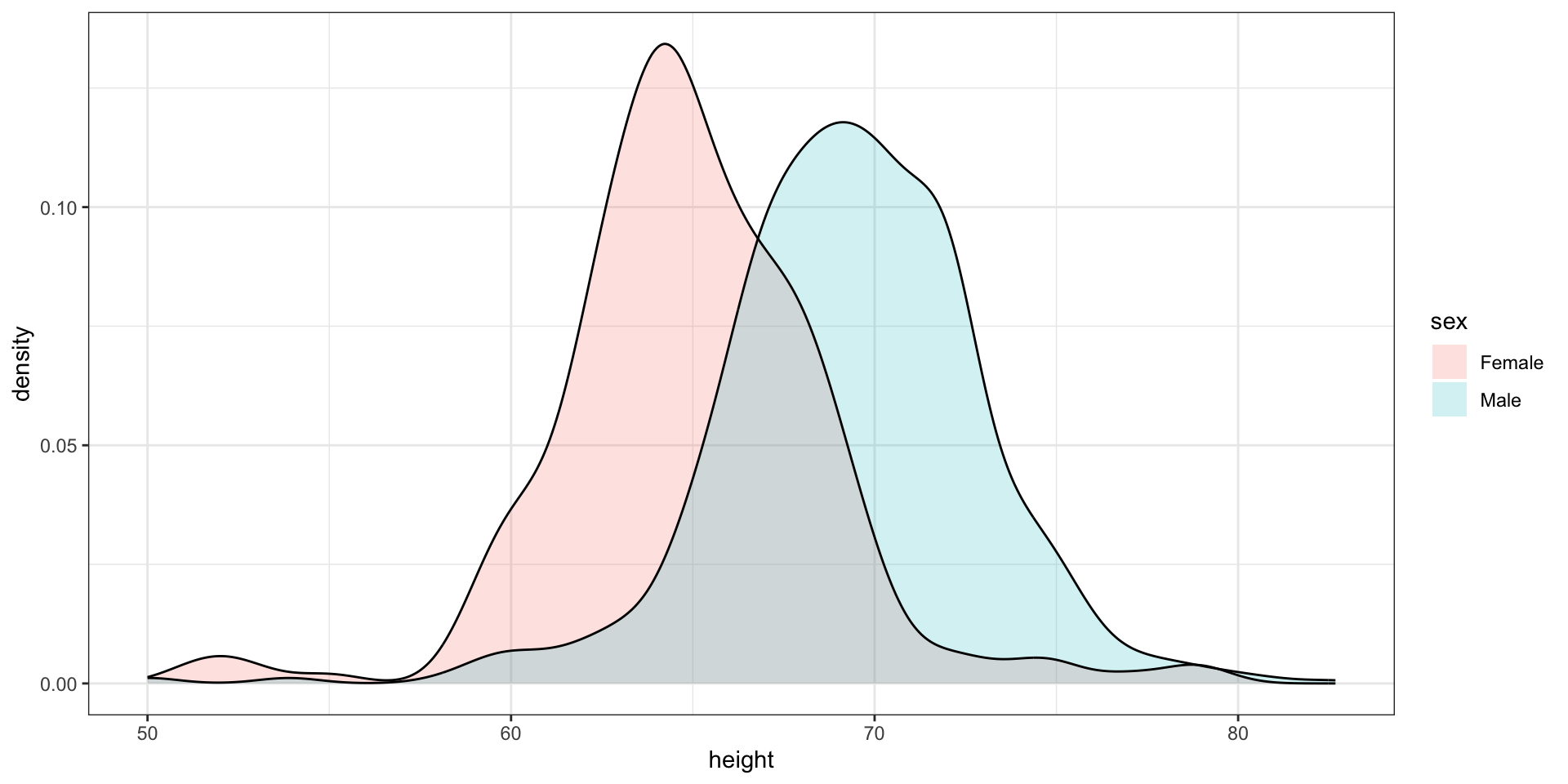
The normal distribution

  • Histograms and density plots provide excellent summaries of a distribution.

  • But can we summarize even further?

  • We often see the average and standard deviation used as summary statistics

  • To understand what these summaries are and why they are so widely used, we need to understand the normal distribution.

The normal distribution

  • The normal distribution, also known as the bell curve and as the Gaussian distribution.

The normal distribution

  • Many datasets can be approximated with normal distributions.

  • These include gambling winnings, heights, weights, blood pressure, standardized test scores, and experimental measurement errors.

  • But how can the same distribution approximate datasets with completely different ranges for values?

The normal distribution

  • The normal distribution can be adapted to different datasets by just adjusting two numbers, referred to as the average or mean and the standard deviation (SD).

  • Because we only need two numbers to adapt the normal distribution to a dataset implies that if our data distribution is approximated by a normal distribution, all the information needed to describe the distribution can be encoded by just two numbers.

  • A normal distribution with average 0 and SD 1 is referred to as a standard normal.

The normal distribution

  • For a list of numbers contained in a vector x:
index <- heights$sex == "Male" 
x <- heights$height[index]
  • the average is defined as.
m <- sum(x) / length(x) # or mean(x)
  • and the SD is defined as:
s <- sqrt(sum((x - m)^2) / length(x)) # or sd(x)

Warning

sd(x) is the sample standard deviation which is not exactly the same as the standard deviation.

For reasons explained in later,sd divides by length(x)-1 rather than length(x) can be used here:

n <- length(x)
sd(x)^2*(n - 1)/n - sum((x - mean(x))^2)/n
[1] -3.55e-15

The normal distribution

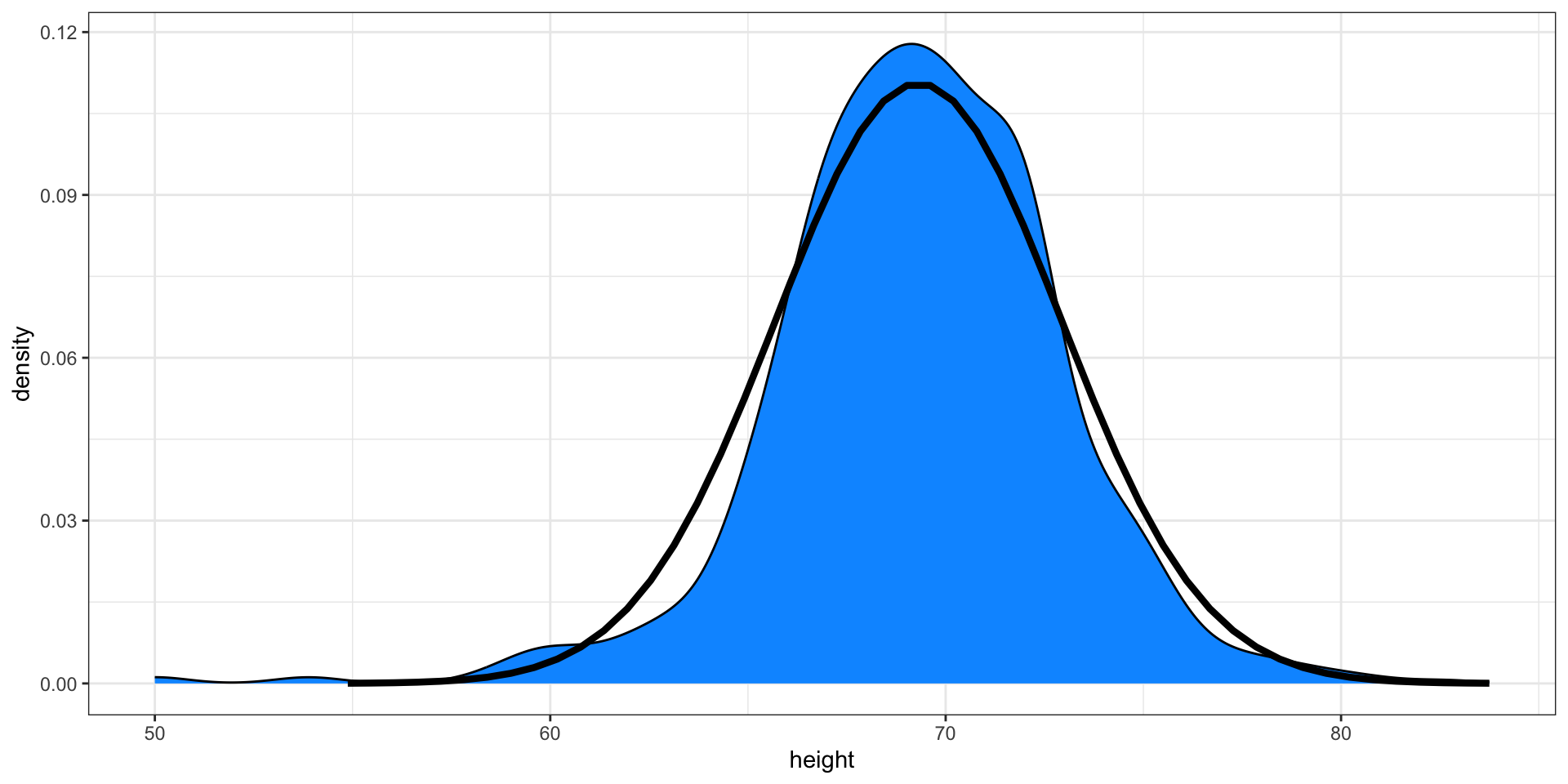
  • Here is a plot of our male student height smooth density (blue) and the normal distribution (black) with mean = 69.3 and SD = 3.6:

Boxplot

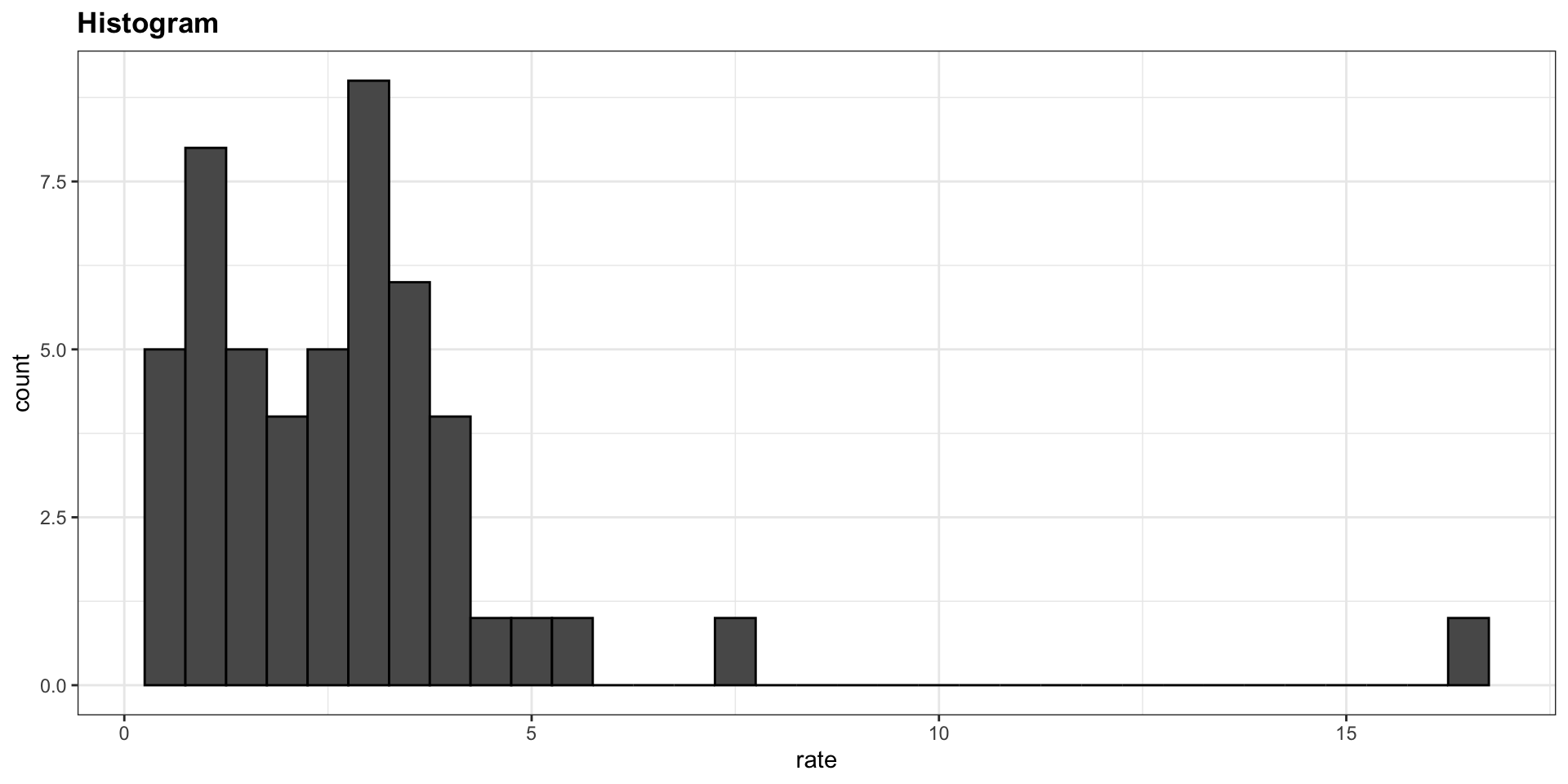
  • Suppose we want to summarize the murder rate distribution.

Boxplots

  • In this case, the histogram above or a smooth density plot would serve as a relatively succinct summary.

  • But what if we want a more compact numerical summary?

  • Two summaries will not suffice here because the data is not normal.

Boxplots

  • The boxplot provides a five-number summary composed of the range (the minimum and maximum) along with the quartiles (the 25th, 50th, and 75th percentiles).

  • The R implementation of boxplots ignore outliers when computing the range and instead plot these as independent points.

  • The help file provides a specific definition of outliers.

Boxplots

The boxplot sumarizes with a box with whiskers:

From just this simple plot, we know that:

  • the median is about 2.5,
  • that the distribution is not symmetric, and that
  • the range is 0 to 5 for the great majority of states with two exceptions.

Boxplots

  • In data analysis we often divide observations into groups based on the values of one or more variables associated with those observations.

  • We call this procedure stratification and refer to the resulting groups as strata.

  • Stratification is common in data visualization because we are often interested in how the distributions of variables differ across different subgroups.

  • Stratifying and then making boxplot is a common approach to visualizing these differences.

Case study continued

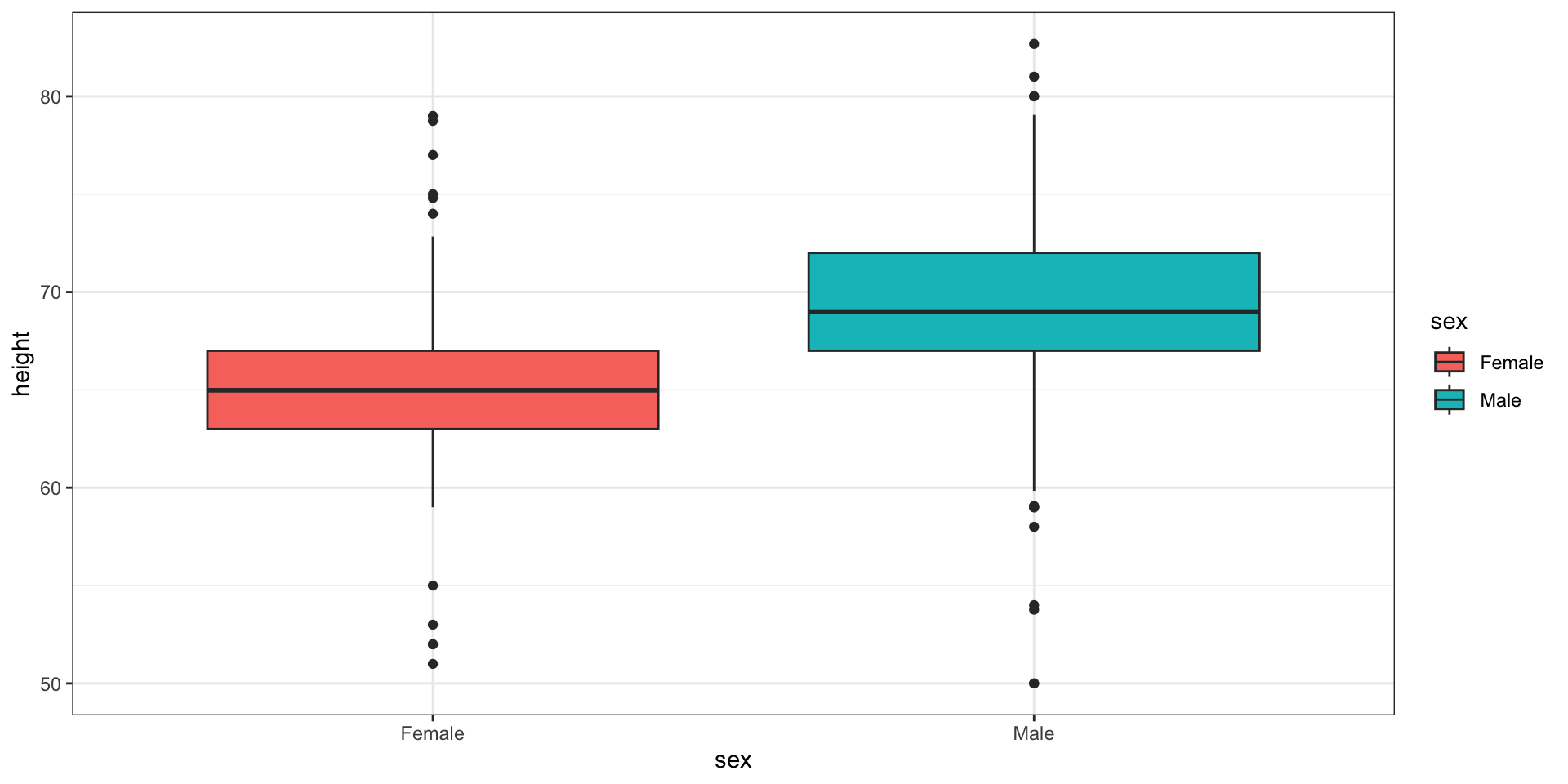
Here are the heights for men and women:

Case study continued

  • The plot immediately reveals that males are, on average, taller than females.

  • However, exploratory plots reveal that the approximation is not as useful:

Case study continued

  • A likely for the second bump is that female as the default in the reporting tool.

  • The unexpected five smallest values are likely cases of 5'x'' reported as 5x

[1] 51 53 55 52 52